[Algorithm] Brute Force
Brute Force Search(브루트포스)
아마도 알고리즘을 공부하면서 가장 처음으로 뭔가… 알고리즘 같은? 것을 배우기 시작하는 부분이 아닐까 싶다.
흔히들 그냥 브루트 포스라고 부르지만 알고리즘이므로 Search 가 붙는 것이 맞다고 본다.
Brute Force(브루트 포스) : 야만적인 힘
즉, 무식하게 모든 경우를 다 탐색해본다는 뜻이다. 모든 경우를 다 탐색하는 만큼 거의 틀릴 일 없이 정확하다. 하지만, 그만큼 많은 시간복잡도 와 공간복잡도 를 갖는다.
작년 이맘때 즈음 알고리즘 공부를 시작하면서 무작정 부딪혔을때가 생각난다. 상반기 시즌이 얼마 남지 않았어서 속성으로 공부하고 있을때여서 확실한 이해도 없이 문제를 풀었었던… 간단한 문제들 조차 며칠씩 걸려서 문제를 풀고 너무 힘들었던 … ㅠㅜ (지금도 힘들다.)
당시에 풀었던 문제를 리뷰해보자.
일곱 난쟁이
문제 요약
100을 넘지않는 9개의 정수가 주어지고 9개 중 7개의 정수의 합이 100이 되는 경우를 찾아 그 7개의 정수를 출력하라.
문제 설명
$_9C_7$ 이 되는 모든 경우의 수를 구하여라.
즉, 9명의 난쟁이 중 키의 합이 100이 되는 7명을 찾아라. 라는 문제이다.
문제 풀이
예전 코드
#include<iostream>
using namespace std;
const int MAX_HEIGHT = 100;
int dwarf[9];
int Sum;
void Input() {
for (int i = 0; i < 9; i++) {
cin >> dwarf[i];
Sum += dwarf[i];
}
}
void Find7Dwarfs(int i, int j) {
int find7 = Sum - (dwarf[i] + dwarf[j]);
if (MAX_HEIGHT == find7) {
dwarf[i] = -1;
dwarf[j] = -1;
return;
}
if (j == 8) {
i++;
j = i + 1;
}
else j++;
Find7Dwarfs(i, j);
}
void Swap(int *a, int *b) {
int t = *a;
*a = *b;
*b = t;
}
void QuickSort(int left, int right, int *data) {
int pivot = left;
int j = pivot;
int i = left + 1;
if (left < right) {
for (; i <= right; i++) {
if (data[i] < data[pivot]) {
j++;
Swap(&data[j], &data[i]);
}
}
Swap(&data[left], &data[j]);
pivot = j;
QuickSort(left, pivot - 1, data);
QuickSort(pivot + 1, right, data);
}
}
void Process() {
Find7Dwarfs(0, 1);
QuickSort(0, 8, dwarf);
for (int i = 2; i < 9; i++)
cout << dwarf[i] << endl;
}
void Solution() {
Input();
Process();
}
int main() {
Solution();
return 0;
}
와… 이 때는 알고리즘 잘하는 친구 왈 “stl 쓰지말라!” 는 한 마디에 모든걸 구현해서 풀었다.. c와 c++은 그냥 printf, scanf 이냐 cin cout이냐 밖에 없다…
예전 알고리즘 문제들은 stl을 사용하지 못하게하는 시험들이 많았다라고는 했었는데.. 1년의 경험상 무쓸모다 쓸 수있는 stl은 쓰자! 대신 구조와 작동방식은 정확하게 알고 가자.
대충 기억을 더듬어 보면 재귀함수를 이용하여 모든 경우를 구했다.
- 9개의 정수를 입력 받으며 전체 합을 구한다.
- 9개 중 2개씩 선택하며 선택한 두 수를 총 합에서 빼고 100인지 확인한다.
- 그림 설명.
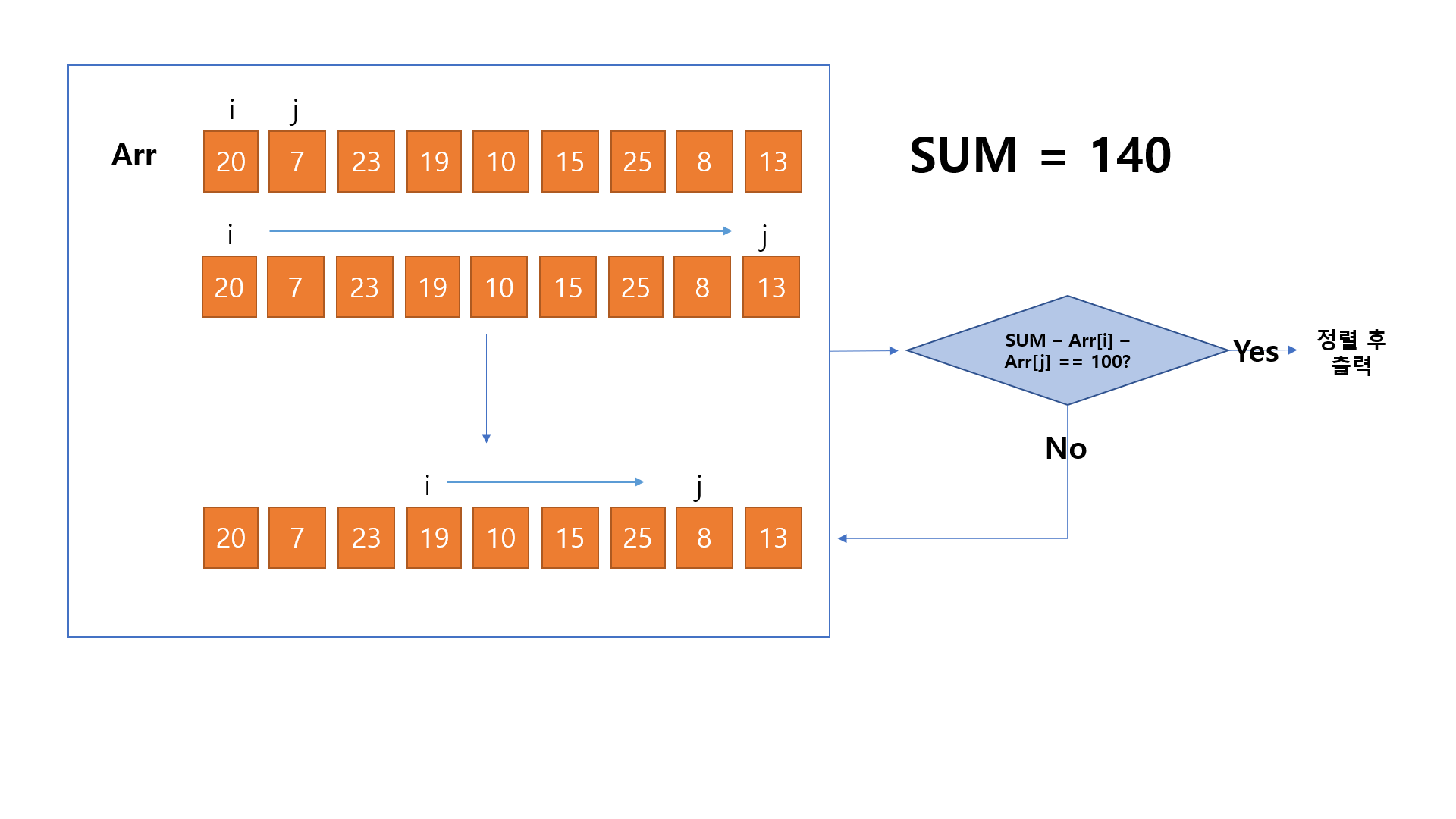
- 위 그림과 같이 i와 j를 하나씩 증가해주면서 조건에 맞는 결과를 찾을 때 까지 반복한다.
dp 나 좀 더 최적화 시킬 방법 을 찾다가 문제 자체가 그냥 완탐을 하라는 문제인거 같아서 고민하다가 그냥 완전탐색으로 구현하였다. 그리 복잡한 문제도 아니고 해서 재귀를 사용하지 않고 반복문으로 해결하였다.
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int main() {
vector<int> v;
int sum = 0;
for (int i = 0; i < 9; i++) {
int a; cin >> a;
v.push_back(a);
sum += a;
}
vector<int> answer;
for (int i = 0; i < 9; i++) {
for (int j = i + 1; j < 9; j++) {
if (sum - v[i] - v[j] == 100) {
for (int k = 0; k < 9; k++) {
if (k != i && k != j) {
answer.push_back(v[k]);
}
}
sort(answer.begin(), answer.end());
for (auto ans : answer)
cout << ans << endl;
return 0;
}
}
}
return 0;
}
그렇다면 Brute Force 와 Dynamic Procramming 둘 다 풀 수 있는 문제를 보자.
예전에 올렸던 퇴사 문제다. 문제 설명은 아래 링크를 통해 알아보자.
퇴사 문제를 Brute Force 로풀고나서 나중에 DP 로도 풀 수 있다는 것을 알게됐었지만 다시 풀어야지 하면서 미루다가 이번 기회에 DP 방식으로 다시 한 번 풀어보았다.
#include <iostream>
#include<algorithm>
#include<vector>
#define PII pair<int,int>
using namespace std;
const int MAX = 15;
const int INF = 1 << 30;
int N;
vector<PII> info; //Ti, Pi
vector<int> dp;
int solution(int day) {
if (day == N )return 0;
if (day > N )return -INF;
if (dp[day])return dp[day];
else
return max(solution(day + 1), solution(day + info[day].first) + info[day].second);
}
int main() {
cin >> N;
for (int i = 0; i < N; i++) {
int t, p;
cin >> t >> p;
info.push_back({ t,p });
}
dp.assign(N, 0);
cout << solution(0) << endl;
return 0;
}
사실 문제 자체가 DP 를 이용할 만큼을 요구하지 않아서인지 결과의 차이는 없었다.
Brute Force 로 풀었을 때 걸리는 최악의 시간복잡도는 $O(N^2)$
DP 로 풀었을 때 걸리는 최악의 시간복잡도는 $O(N)$
하지만 결과는 차이가 없다.
문제 풀이
DP 풀이는 이전에 계산된 값을 memoization 을 통해 다시 한 번 계산되지 않게하여 필요 없는 계산을 줄인다.
if (dp[day])return dp[day];
else
return max(solution(day + 1), solution(day + info[day].first) + info[day].second);
이 부분이 핵심이다. dp[day]에 값이 있으면 그냥 그 값을 return하고 그렇지 않다면 day+1을 했을 때 나오는 값과 그 날 일을 했을 때의 값을 비교하여 최댓값으로 갱신 해준다.
dp에 대한 자세한 설명은 다음 포스팅에서 다루겠다.

댓글남기기