[algorithm] 힙(heap) 이란?

자료구조 힙(heap)이란?

먼저 완전 이진 트리 가 무엇인지 알아보자. 완전 이진 트리 는 데이터 루트(Root) 노드부터 시작해서 자식 노드가 왼쪽, 오른쪽 노드로 차근차근 들어가는 구조의 이진 트리 이다.

힙(heap) 은 이 완전 이진 트리를 이용하여 최솟값이나 최댓값을 빠르게 찾아낼 수 있는 자료구조이다.

힙(heap)의 종류

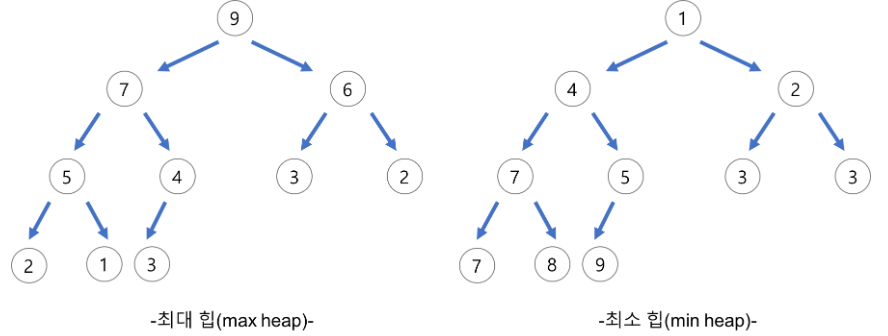
• 최대 힙(Max Heap)
  • 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진트리
  • key(부모 노드) >= key(자식 노드)
• 최소 힙(Min Heap)
  • 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진트리
  • key(부모 노드) <= key(자식 노드)

힙(heap)의 구현

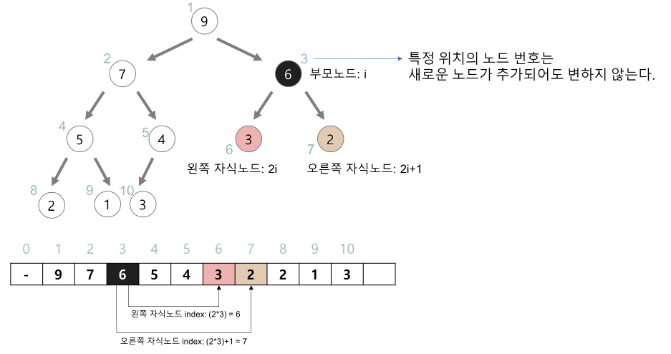
배열을 이용하여 편의를 위하여 1번 인덱스부터 작성한다. 힙에서 부모 노드와 자식 노드의 관계

• 왼쪽 자식 노드 인덱스 = (부모 인덱스) * 2
• 오른쪽 자식 노드 인덱스 = (부모 인덱스) * 2 + 1
• 부모 인덱스 = (자식 노드) / 2

)

)

#include<cstdio>

int num = 9;
int heap[9] = { 7,6,5,8,3,5,9,1,6 };

int main() {
	//트리 구조를 최대 힙 구조로 바꿈
	for (int i = 1; i < num; i++) {
		int c = i;
		do {
			int root = (c - 1) / 2;
			if (heap[root] < heap[c]) {
				int tmp = heap[root];
				heap[root] = heap[c];
				heap[c] = tmp;
			}
			c = root;
		} while (c != 0);
	}
	//크기를 줄여가며 반복적으로 힙 구성
	for (int i = num - 1; i >= 0; i--) {
		int tmp = heap[0];
		heap[0] = heap[i];
		heap[i] = tmp;
		int root = 0;
		int c = 1;
		do {
			c = 2 * root + 1;
			//자식 중에 큰 값을 찾기
			if (heap[c] < heap[c + 1] && c < i - 1) {
				c++;
			}
			// 루트 보다 자식이 크다면 교환
			if (c < i&&heap[root] < heap[c]) {
				tmp = heap[root];
				heap[root] = heap[c];
				heap[c] = tmp;
			}
			root = c;
		} while (c < i);
	}
	for (int i = 0; i < num; i++)
		printf("%d ", heap[i]);

	return 0;
}

참조 :

• https://m.blog.naver.com/ndb796/221228342808
• https://twpower.github.io/137-heap-implementation-in-cpp