[프로그래머스]2 x n 타일링

프로그래머스 문제도 정복해보자. 프로그래머스 코딩테스트연습에 있는 문제들 중 lv3~lv5까지의 문제만 쭈욱 풀어보기로 했다.
평소 백준이나 삼성 기출 문제 형식에 익숙해져있어서 프로그래머스 문제는 같은 문제라도 좀 느낌이 달랐다. 아직까지도 STL사용에 익숙하지 않아서 그런 것 같다. 프로그래머스 문제들은 main함수, 예시 입력 부분은 건드릴 필요 없이 문제에 대한 논리적 풀이 과정만을 작성하면된다. 크게 다를 것은 없지만… 뭔가 더 어렵다.. 익숙해져 보자.

한 달 전부터 시작했는데 좀 바빠서 미뤄뒀더니 문제가 너무 많이 쌓여버렸다… 미루지말자 ㅠㅜ

(lv3) 2 x n 타일링

문제

예전에 DP(다이나믹프로그래밍를 살짝 공부하면서 풀어봤던 문제이다. 이 문제를 통해서 memoization이 뭔지 알게됐다. 나중에 DP(다이나믹프로그래밍에 대해 포스팅을 해야겠다.

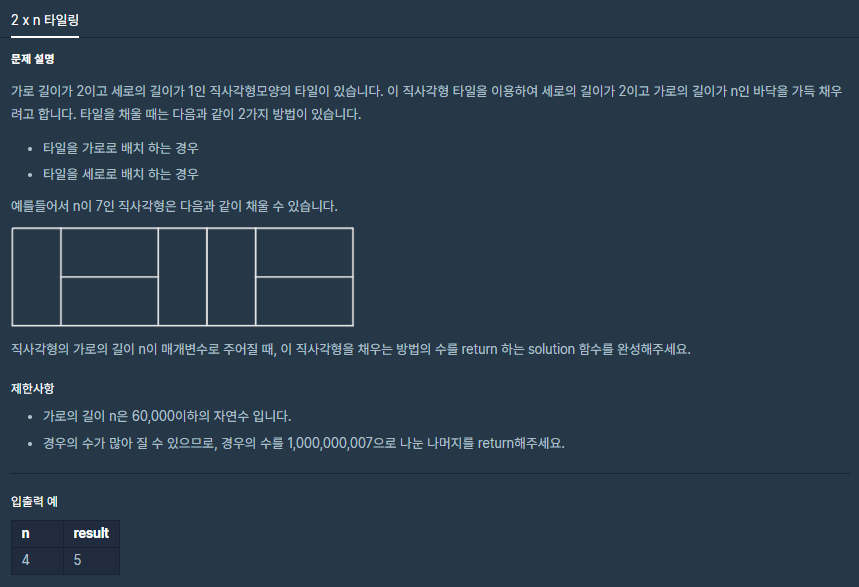
문제 풀이

위 그림과 같이 (1 x 2) 나 (2 x 1)의 타일로 2 x n을 채울 수 있는 모든 방법의 수를 구하는 문제이다. DP라는 개념을 전혀 모를 때 처음 문제를 접했을 때는 엄청 답답했다. 엄청나게 많을건데 이걸 어떻게 구하지? 너무 막막했다.
DP(다이나믹 프로그래밍)은 간단히 말하면 큰 문제 를 작은 문제 로 나누어 해결하는 방법이다. 결국 규칙을 찾아 해결하는 문제이다.

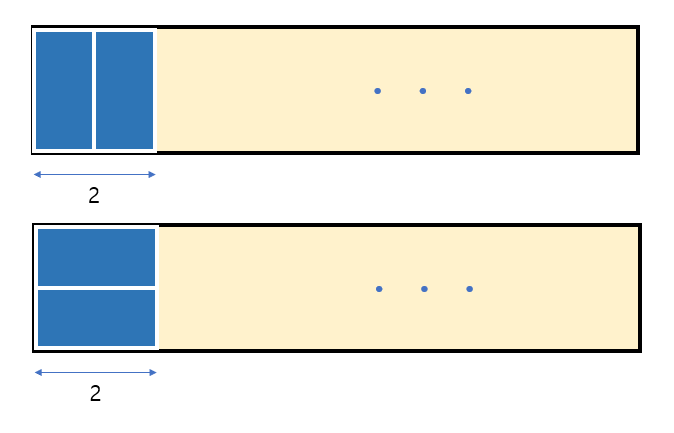
길이가 2일 때 블럭을 채우는 방법은 위 그림과 같다. 잘 생각해보면 이 막대를 채울 때 방법이 2가지밖에 없다. 무슨말이냐면 (2 x 1) 를 1개 채우는 방법과, (1 x 2)를 2개 채우는 방법 2가지 밖에 없다. 이 2가지 방법을 길이 n에 맞게 조합하여 세우는 방법의 수가 결국 이 문제의 답이 된다.
다음의 예를 보자.

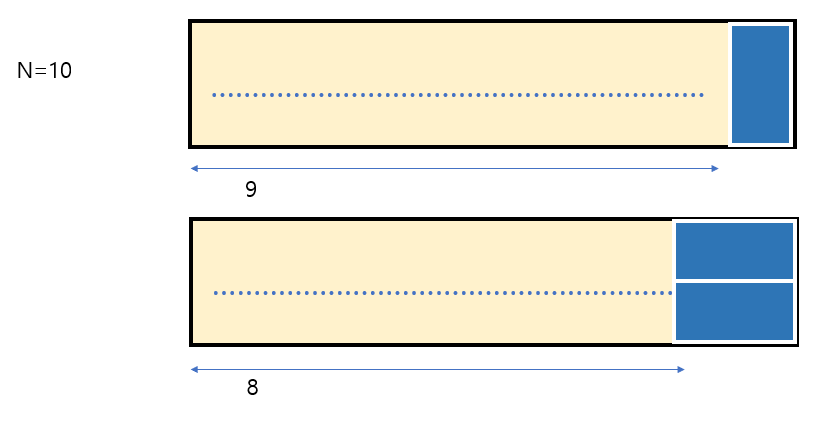
N = 10이라면 결국 마지막에 채울 블럭의 방법은 아래 두가지 방법밖에 없다. 따라서 위의 경우에는 N=9일 때의 경우의 수와 동일하고, 아래의 경우에는 N=8일 때의 경우의 수와 동일하다. 이런 규칙을 통해서 점화식을 세우면 아래와 같다.

$f(10) = f(9) + f(8)$
$because$
$f(N) = f(N-1) + f(N-2)$ 이 과정을 재귀함수를 이용하여 memoization하게 되면
$f(1) = 1, f(2) = 2$ 를 미리 dp[1] = 1, dp[2] = 2라고 저장시켜 둔 후 n=3일 때부터 위의 규칙을 이어 나가면 이 문제를 해결할 수 있다.

설명은 길었지만 코드는 간단하다.

#include<iostream>
#include<vector>

using namespace std;
int N;
int dp[60001];
int solution(int n) {
	if (n == 1)return dp[n] = 1;
	else if (n == 2)return dp[n] = 2;
	if (dp[n])return dp[n];
	else return dp[n] = solution(n - 1) + solution(n - 2);
}
int main() {
	cin >> N;
	solution(N);
	cout << dp[N] << "\n";
	return 0;
}