[프로그래머스]3 x n 타일링

(lv4) 3 x n 타일링

문제

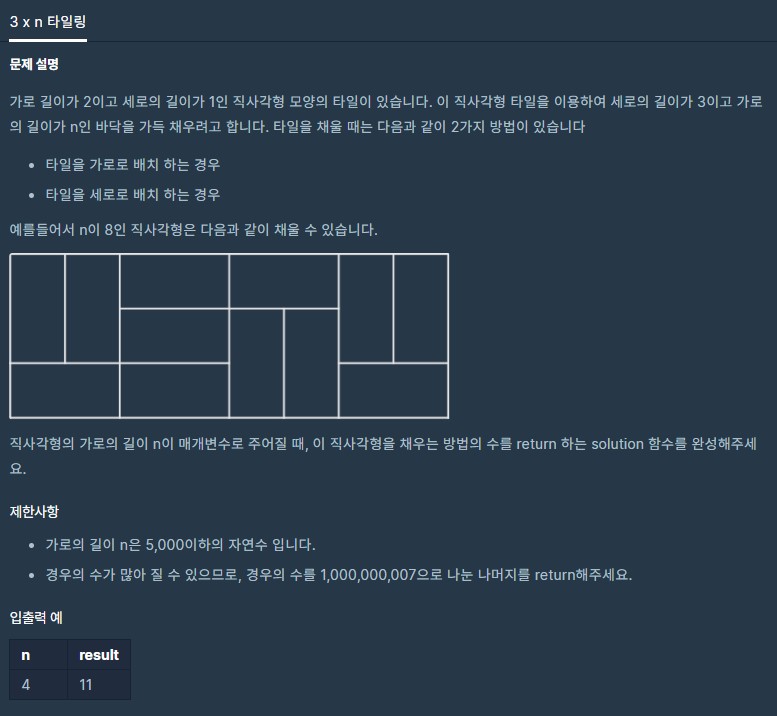
2xn 타일링의 업그레이드 버전이다. 무려 lv 4 … 규칙을 찾아도 생각을 많이 해야했던 문제이다.

문제 풀이

이번에는 위 그림과 같이 (1 x 2) 나 (2 x 1)의 타일로 3 x n을 채울 수 있는 모든 방법의 수를 구하는 문제이다.
어떤 규칙이 있을까…
2xn 타일링문제와 같이 n까지 채울 수 있는 방법에 대해 고민해봤다.
잘 생각해보면 이 문제는 N이 홀수 일 때에는 주어진 타일들로 채울 수 있는 방법이 없다. 따라서 N이 짝수 인 경우만 생각해보자.
N=4인 경우 (2, 2)와 4로 만들 수 있는 경우가 있다. N=2를 만들 수 있는 방법은 총 3가지 이므로 (2, 2)로 만들 수 있는 방법은 3 x 3 = 9가지, 4로 만들 수 있는 새로운 모양 2가지를 더하여 총 11가지가 있다.

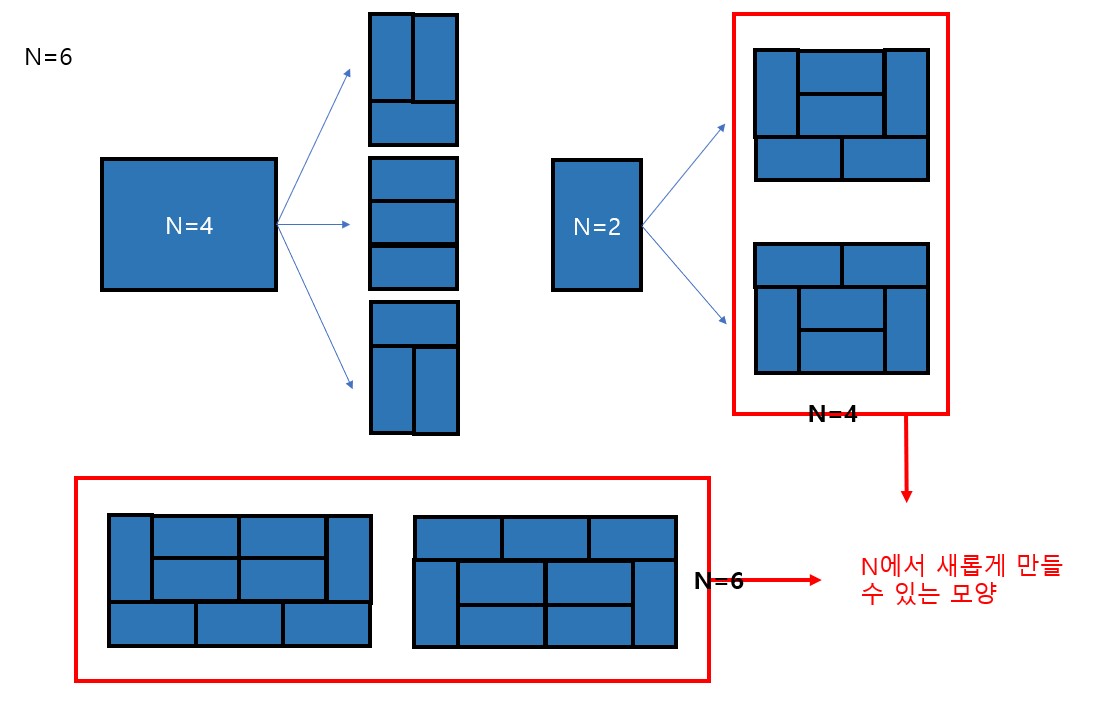
N=6일 때를 그림으로 위 설명을 보충해자.
N=6을 만들 수 있는 방법은

• N=6에서 새롭게 만들 수 있는 모양 2가지
• N=4에 N=2를 만들 수 있는 방법의 곱 33가지
• N=2에 N=4에 새롭게 만들수 있는 모양 2가지의 곱 6가지
• 총 41가지가 된다.

이런식으로 규칙을 찾아주면 $f(4) = 3f(2) + 2$
$f(6) = 3f(4) + 2f(2) + 2 $
$f(8) = 3f(6) + 2f(4) 2f(2) + 2 $
$because$
$f(N) = 3f(N-2) + 2f(N-4) + 2f(N-6) + … + 2f(2) + 2$
라는 규칙을 찾을 수 있다.
여기서 N-4부터 2를 곱하는 이유는 N에서 N-a(a= 4, 6, 8, …)를 채우고 남은 부분에 a만큼에 새로 만들 수 있는 모양은 모두 2가지 뿐이어서 이다. 이 때 맨 마지막 2(즉 N으로 만들 수 있는 새로운 모양) 이라고 생각하여 $f(0)=1$이라고 미리 저장해두면 for문을 이용하여 규칙성을 가지는 식을 만들 수 있다.

#include<iostream>
using namespace std;
const int MOD = 1000000007;
long long dp[5001];
long long process(int n) {
	if (n == 0) return 1;
	if (n == 1)	return 0;
	if (n == 2) return 3;
	if (dp[n]) return dp[n];
	else {
		dp[n] = 3 * process(n - 2);
		for (int i = 4; i <= n; i += 2) {
			dp[n] += 2 * process(n - i);
		}
		dp[n] %= MOD;
		return dp[n];
	}
}
int solution(int n) {
	int answer = 0;
	answer = process(n);
	return answer;
}