[프로그래머스]섬 연결하기

(lv3) 섬 연결하기

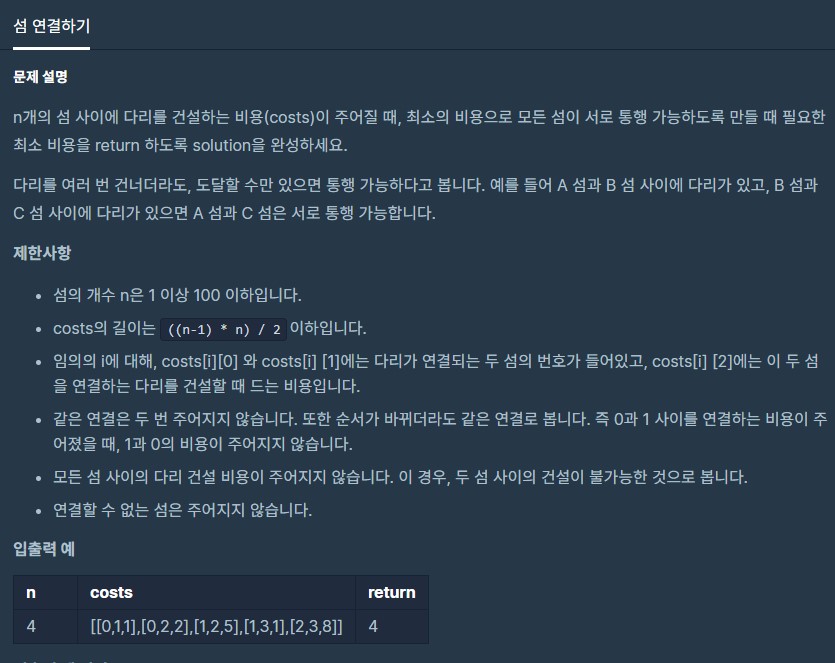
문제

기존에 최소 신장 트리 라는 개념은 얄팍하게나마 알고있었지만 문제로서는 처음 접했던 문제인 것 같다.
최소 신장 트리 는 MST 라고도 불리는데 각 정점들과 연결 된 간선에 가중치가 있을 때 조건에 맞게 그래프를 이동하며 비용이 최소가 되는 트리를 만드는 방법이다. 이런 문제를 해결할 수 있는 방법에는

• Kruskal 알고리즘 :탐욕적인(greedy) 방법을 이용하여 그래프의 모든 정점을 최소 비용으로 연결하는 최적해를 구하는 것
• Prim 알고리즘 : 시작 정점에서부터 출발하여 ST(Spanning Tree) 집합을 단계적으로 확장해나가는 방법

이 두가지가 대표 적이다. 나는 이 문제를 크루스칼 알고리즘을 이용하여 풀어보았다.

문제 풀이

#include<iostream>
#include <string>
#include <vector>
#include<algorithm>

using namespace std;
//parents[i] 정점 i의 부모 정점을 보관
int parents[101];

bool compare(const vector<int> &a, const vector<int> &b) {
	return a[2] < b[2];
}
//최상위 부모를 찾는 함수
int find(int node) {
	//부모노드가 자기자신이면 현재 노드가 최상위 노드
	if (node == parents[node])return node;
	//아니라면 최상위 부모노드를 찾음
	else {
		parents[node] = find(parents[node]);
		return parents[node];
	}
}
int solution(int n, vector<vector<int>> costs) {
	int answer = 0;
	//처음에는 모두 자기자신이 부모노드
	for (int i = 0; i < n; i++) parents[i] = i;
	//가중치 오름차순 정렬
	sort(costs.begin(), costs.end(), compare);

	for (int i = 0; i < costs.size(); i++) {
		int start = find(costs[i][0]);
		int end = find(costs[i][1]);
		int cost = costs[i][2];

		//start와 end가 연결되어있지 않다면
		if (start != end) {
			//start의 부모를 end
			parents[start] = end;
			//간선의 가중치 누적
			answer += cost;
		}
	}
	
	return answer;
}