[SWEA]삼성모의기출 - 등산로 조성

삼성 모의 역량 테스트

문제 : 등산로 조성

문제설명

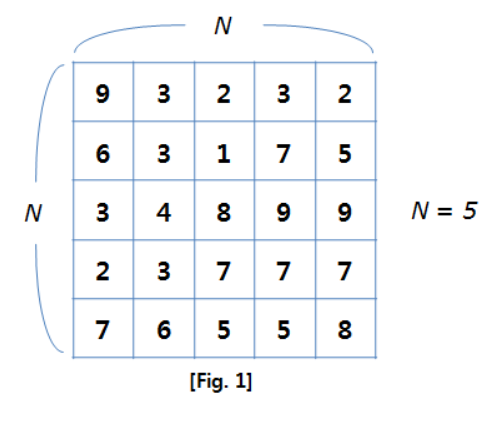
등산로를 만들기위한 부지는 N * N 크기를 가지고 있으며, 최대한 긴 등산로를 만들려고 한다. 각 숫자는 지형의 높이를 나타낸다.

등산로 조성 규칙

1. 등산로는 가장 높은 봉우리에서 시작해야 한다.
2. 등산로는 산으로 올라갈 수 있도록 반드시 높은 지형에서 낮은 지형으로 연결되어야 한다. (대각선 x)
3. 긴 등산로를 만들기 위해 딱 한 곳 을 정해서 최대 K 깊이 만큼 지형을 깎는 공사를 할 수 있다.

제약사항

1. 시간 제한 : 50개의 테스트를 모두 통과하는데 3초
2. 지도 한 변의 크기 3 $\le$ N $\le$ 8
3. 최대 공사 가능 깊이 1 $\le$ K $\le$ 5
4. 1 $\le$ 지형의 높이 $\le$ 20
5. 지형에서 가장 높은 부분 최대 5개
6. 필요한 경우 지형을 1보다 작게 깎을 수 있다

문제풀이

2019 윈터코딩 지형 이동 문제와 비슷한 것 같다. 아직 해결하지 못했던 문제인데 다시 한번 풀어봐야겠다.

1. 등산로는 적어도 하나 이므로 ans = 1로 초기화 해준다.
2. 지도 정보를 입력 받으면서 최대 높이를 maxHeight에 갱신해 준다.
3. maxHeight를 이용하여 지도의 모든 칸을 돌며 가장 높은 부분을 찾아 dfs 를 실행해준다.
4. process함수에 필요한 인자는 탐색할 현재 위치, 등산로의 길이, 공사 여부 가 있다.
   DFS
5. ans에 최대 길이를 항상 갱신해 준다.
6. 현재 좌표의 4방향에 대해서 탐색을 한다. 다음 좌표가 지도 범위안에 들고, 방문하지 않은 곳이고, 현재 지형이 다음 지형보다 크다면 다음 좌표로 방문한다.
7. 현재 지형보다 다음 지형보다 작고, 공사를 하지 않은 부분이라면 공사를 진행한다.
8. 공사를 진행할 때에는 깊이가 1~K까지 한 칸씩 늘려가며 내리막길이 되는지 안되는지 체크를 하며 진행한다.
   /DFS
9. 위 DFS 과정을 반복한다.

#include<iostream>
#include<vector>
#include<queue>
#include<algorithm>
#define endl "\n"
using namespace std;

const int MAX = 8;

int Map[MAX][MAX];
bool visit[MAX][MAX];
int N, K, maxHeight, ans;
int dx[] = { 1,0,-1,0 };
int dy[] = { 0,1,0,-1 };

// dfs
void process(int x, int y, int len, bool isK) {
	ans = max(ans, len);
	//Pos cur = { x,y };
	for (int i = 0; i < 4; ++i) {
		//int nx = cur.x + dx[i], ny = cur.y + dy[i];
		int nx = x + dx[i], ny = y + dy[i];

		if (nx >= 0 && nx < N&&ny >= 0 && ny < N) {
			// 내리막길
			if (!visit[ny][nx]) {
				if (Map[y][x] > Map[ny][nx]) {
					visit[ny][nx] = true;
					process(nx, ny, len + 1, isK);
					visit[ny][nx] = false;
				}
				// 내리막길 x , 공사 안함
				else if (Map[y][x] <= Map[ny][nx] && !isK) {
					//공사 진행
					for (int dig = 1; dig <= K; ++dig) {
						isK = true;
						Map[ny][nx] -= dig;
						if (Map[y][x] > Map[ny][nx]) {
							visit[ny][nx] = true;
							process(nx, ny, len + 1, isK);
							visit[ny][nx] = false;
						}
						Map[ny][nx] += dig;
						isK = false;
					}
				}
			}
		}
	}
}
void solution() {
	for (int i = 0; i < N; ++i) {
		for (int j = 0; j < N; ++j) {
			if (maxHeight == Map[i][j]) {
				visit[i][j] = true;
				process(j, i, 1, false);
				visit[i][j] = false;
			}
		}
	}
}
int main() {
	cin.tie(NULL);
	ios::sync_with_stdio(false);
	freopen("swea_1949.in", "r", stdin);
	int T;
	cin >> T;
	for (int tc = 1; tc <= T; tc++) {
		/*---- Init ----*/
		cin >> N >> K;
		for (int i = 0; i < N; i++) {
			for (int j = 0; j < N; j++) {
				Map[i][j] = 0;
				visit[i][j] = false;
			}
		}
		ans = 1;
		maxHeight = 0;
		/*---- Init ----*/

		for (int i = 0; i < N; ++i) {
			for (int j = 0; j < N; ++j) {
				cin >> Map[i][j];
				maxHeight = max(maxHeight, Map[i][j]);
			}
		}
		solution();
		cout << "#" << tc << " " << ans << endl;
	}

	return 0;
}